mg视讯平台游戏介绍AG平台游戏规则
mg 视讯平台游戏介绍,AG平台游戏规则
 ————点击图片进入游戏——————
炸金花是常见的一种扑克游戏,类似于德州扑克的简化版本。
————点击图片进入游戏——————
炸金花是常见的一种扑克游戏,类似于德州扑克的简化版本。
考虑最简单的2人情形,双方各下了1元的底注,假设游戏只存在1回合的博弈。我方先看牌,选择弃牌或者加注,如果我方没弃牌,对方看牌后选择弃牌或者比牌。双方应该如何选择策略来最大化自身收益呢?
虽然这种特殊情形,已经大大简化问题的复杂度了,但策略计算依然并不简单。
双方手牌的大小分别设为x和y,它们服从区间[0,1]上的均匀分布。典型策略是设置一个关键点,比如我方设定0.4为关键点,那么只要手牌小于0.4就直接弃牌,高于0.4则加注。对方则根据我方加注的额度来决定某个大小为关键点。假设我方的关键点是
,加注额度是手牌大小
的函数
,对方的关键点是
.
采用以上博弈策略,我方收益的数学期望可以用以下方式计算。涉及到2个独立均匀分布,用图示更直观一点:
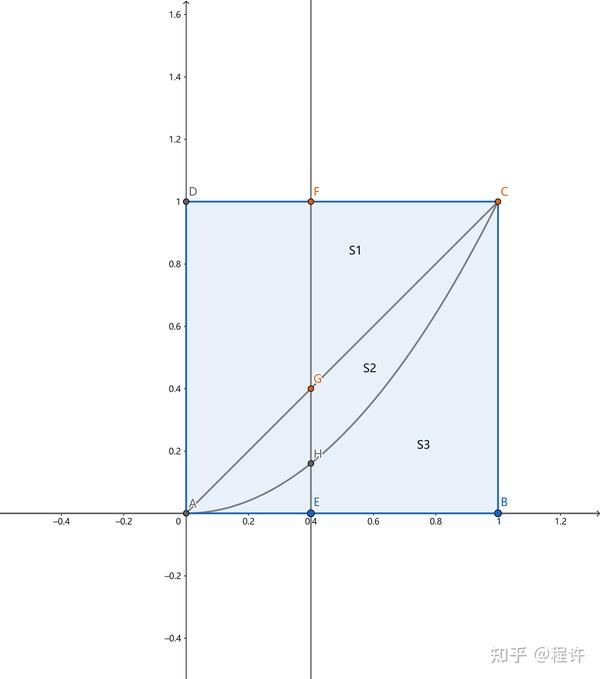
平均收益的图示横轴为我方手牌大小,纵轴为对方手牌大小。直线EF代表我方关键点对应的分割直线
,
对应的区域
代表我方加注
,对方选择比牌,我方输了。这时我方收益为
.这里算收益的时候,默认底注是沉默成本,不计入损失。
曲边三角形
对应的区域
代表我方加注
,对方选择比牌,我方赢了。这时我方收益为
曲边四边形
对应的区域
代表我方加注
,对方直接弃牌。这时我方收益为2
我方的平均收益P,就是对应区域收益关于该区域的二重积分。

计算这些二重积分时,统一先对
求积,再对
求积,可得

对y求积分可得

整理可得

如果假如给定
,如何选择
才能使得我方平均收益最大化呢?其实这是典型的变分问题,P可视为函数
的变分泛函。根据欧拉-拉格朗日方程可得极值条件为

反过来,对方如何选择
使得我方收益P取得极小值呢?那就把P的积分变量变换成a
利用上面的临界条件,两边求导,可得(导数是对a的求导)

P可以改写为


注意到

所以如果令
,就转化为求泛函极值

再次使用欧拉-拉格朗日方程,可得极值条件:

显然可得
,从而

因此

其中c为待定常数。但此时P可写成

也就是

当
,则选择尽量大的a
根据上面讨论,只需分析双方关键点是常数,且加注金额是常数的简单情形即可。
如果双方关键点分别是
,加注额度为
,分两种情形:
当

为梯形
对应的收益为
,
为
对应的收益为
,
为矩形
对应的收益为2
我方的平均收益就是收益的权重和,权重为对应区域的面积,所以可得:


计算可得

因此当

时P是
的增函数,所以
需要尽量小;
当
时P也是
的增函数,所以
需要尽量小;
当
时,如下图所示:
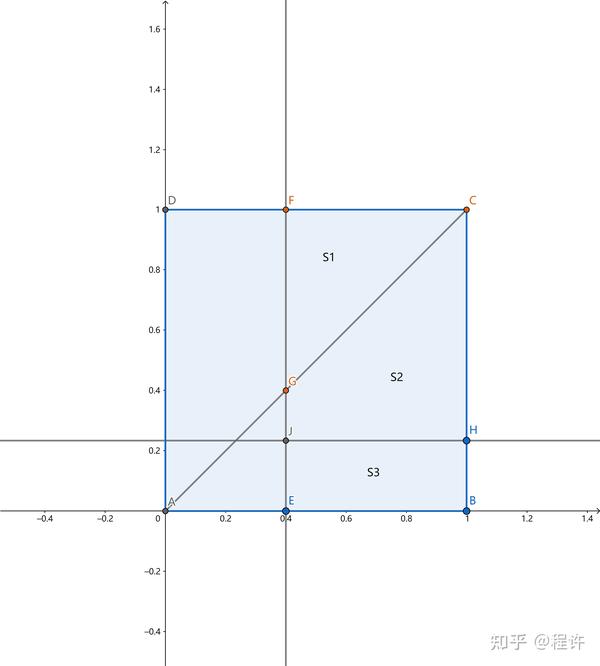

对应的收益依然是
,但对应的区域略有变化,面积需要重新计算:


最终可得:

因此当

我方收益最大化。
对应的对方希望我方收益最小化:

因
,P是减函数,所以
需要尽量大。根据
条件可得
,从而
.由此可得对方最优策略为

双方会在
处形成纳什均衡。
对方
时,我方
,对方
,我方
,对方
,我方...,这个博弈循环会逐渐逼近纳什均衡点。 ————友情链接,https://www.2299yule.com,https://www.2299yule.net,https://www.3344yule.com mg 视讯平台游戏介绍,AG平台游戏规则 澳门赌场,澳门赌场玩法,澳门赌场攻略
考虑最简单的2人情形,双方各下了1元的底注,假设游戏只存在1回合的博弈。我方先看牌,选择弃牌或者加注,如果我方没弃牌,对方看牌后选择弃牌或者比牌。双方应该如何选择策略来最大化自身收益呢?
虽然这种特殊情形,已经大大简化问题的复杂度了,但策略计算依然并不简单。
双方手牌的大小分别设为x和y,它们服从区间[0,1]上的均匀分布。典型策略是设置一个关键点,比如我方设定0.4为关键点,那么只要手牌小于0.4就直接弃牌,高于0.4则加注。对方则根据我方加注的额度来决定某个大小为关键点。假设我方的关键点是
,加注额度是手牌大小
的函数
,对方的关键点是
.
采用以上博弈策略,我方收益的数学期望可以用以下方式计算。涉及到2个独立均匀分布,用图示更直观一点:

平均收益的图示横轴为我方手牌大小,纵轴为对方手牌大小。直线EF代表我方关键点对应的分割直线
,
对应的区域
代表我方加注
,对方选择比牌,我方输了。这时我方收益为
.这里算收益的时候,默认底注是沉默成本,不计入损失。
曲边三角形
对应的区域
代表我方加注
,对方选择比牌,我方赢了。这时我方收益为
曲边四边形
对应的区域
代表我方加注
,对方直接弃牌。这时我方收益为2
我方的平均收益P,就是对应区域收益关于该区域的二重积分。
计算这些二重积分时,统一先对
求积,再对
求积,可得
对y求积分可得
整理可得
如果假如给定
,如何选择
才能使得我方平均收益最大化呢?其实这是典型的变分问题,P可视为函数
的变分泛函。根据欧拉-拉格朗日方程可得极值条件为
反过来,对方如何选择
使得我方收益P取得极小值呢?那就把P的积分变量变换成a
利用上面的临界条件,两边求导,可得(导数是对a的求导)
P可以改写为
注意到
所以如果令
,就转化为求泛函极值
再次使用欧拉-拉格朗日方程,可得极值条件:
显然可得
,从而
因此
其中c为待定常数。但此时P可写成
也就是
当
,则选择尽量大的a
根据上面讨论,只需分析双方关键点是常数,且加注金额是常数的简单情形即可。
如果双方关键点分别是
,加注额度为
,分两种情形:
当
为梯形
对应的收益为
,
为
对应的收益为
,
为矩形
对应的收益为2
我方的平均收益就是收益的权重和,权重为对应区域的面积,所以可得:
计算可得
因此当
时P是
的增函数,所以
需要尽量小;
当
时P也是
的增函数,所以
需要尽量小;
当
时,如下图所示:

对应的收益依然是
,但对应的区域略有变化,面积需要重新计算:
最终可得:
因此当
我方收益最大化。
对应的对方希望我方收益最小化:
因
,P是减函数,所以
需要尽量大。根据
条件可得
,从而
.由此可得对方最优策略为
双方会在
处形成纳什均衡。
对方
时,我方
,对方
,我方
,对方
,我方...,这个博弈循环会逐渐逼近纳什均衡点。 ————友情链接,https://www.2299yule.com,https://www.2299yule.net,https://www.3344yule.com mg 视讯平台游戏介绍,AG平台游戏规则 澳门赌场,澳门赌场玩法,澳门赌场攻略
Comments
Post a Comment